Solving the impossible chessboard puzzle - Part I
In which I transcribe my (almost) unfiltered thought process while solving a puzzle
The impossible chessboard is a beautiful puzzle. The mind-blowing kind of beautiful. When I first heard the instructions, I thought, "That sounds fundamentally impossible". The mere knowledge that a solution existed awakened in me a sense of wonder, a feeling that there is more to this world than meets the eye, and that I would soon uncover some powerful magic.
The puzzle involves two prisoners attempting to communicate information under constrained conditions to find a hidden key, with an adversary present. Before the challenge begins, the prisoners can discuss a strategy, but their adversary will be privy to it. The adversary then hides the key under one of the squares on a chessboard in a private room and arranges coins on each square, either heads up or tails down. The first prisoner is allowed into the room to see the chessboard, is told where the key is hidden, and can flip exactly one coin. They then leave, and the second prisoner enters with the task of determining the location of the key based solely on the arrangement of the coins. The puzzle lies in devising the method for the second prisoner to correctly identify the square under these constraints.
Let's take a moment to appreciate the beauty of this puzzle. Imagine yourself as the second prisoner. You are showed with a chessboard displaying a seemingly random arrangement of coins. You know that one, and only one of these coins has been flipped. Somehow, this single coin flip must have encoded enough information for you to deduce where the key is hidden. One square out of 64 - that is one octet of information that must have been transmitted by flipping a single coin.
Doesn't that seem utterly impossible? The pattern could be completely random. Surely, flipping one bit out of a 64-bit random string still leaves it random, right? Well, not quite. In this case, information theory proves to be a better ally than common sense intuition..
A video from the excellent maths youtuber 3Blue1Brown introduced me to this puzzle. As soon as the puzzle was explained, I stopped the video, knowing that I had to solve it myself. I haven't watched the solution yet.
That gave me an idea: I would record my thought process while solving this problem and write it down "raw" in a blog post. That means including all the dead-ends and silly mistakes - all the things that will sound really stupid in retrospect. I believe sharing my though process will be far more interesting than merely presenting a polished solution (and I doubt that I can do a better job than 3Blue1Brown anyway). So I sat down and started thinking about this puzzle out loud while recording my voice. I quickly generated many ideas and made some progress until eventually, I needed a pen and paper. The notes below represent about one hour working on this problem. I hope you enjoy the journey.
Here is the transcription of my thought process (rephrased for ease of reading):
My first thought was: if as the second player I get a blank board (meaning all the coins on the back side) there is no possibility to transmit information about the position of the key. Well that is not entirely true, we could have agreed beforehand that a blank board means that the key is on the top-left square for example, but let's not go this way for now. What this means is that as the first player, if I see a board with one coin flipped, I should not flip this coin back and produce a blank state. Now, if as the first player I get a blank board, then a simple strategy is to flip the coin where the key is. Great! One case solved already.
Adopting this strategy has implications. It means that if the second player sees a board with a single coin flipped, the key has to be under this coin. What this means is that, as the first player, if I get a board with two coins flipped, I should not go back to a coin with one coin flipped (unless the key is under one of the coins that you were presented). So we already have some rules for the first player:
If the board is blank, flip the coin where the key is
If there is one coin flipped, you have to flip another one (which one?), and somehow this coin's position in relation with the other one must give information on where the key is located
If there are two coins flipped, and the key is under one of these, flip the other one back
If there are two coins flipped, and the key is not under one of these, you have to pick another coin to flip.
The next question is, in situation 2, how do I pick a coin to flip that communicates where is the key... One idea. Can I use the parity of the square on which the key is located? By parity I mean white square or black square. Could we pick for example either the key square or the mirror image of the key square? Could there be some kind of decision process like "if the key is on a black square then the two flipped coins are on different parities and one of them is on top of the key"? What if the key is on a white square? I think I am onto something here.
But what about the case with 3 coins flipped? Oh I have an idea, we could create a 3-way parity of the board. Basically, a modulo operation of the board. [At this point I got lost for a few minutes thinking about how the polarity of position of the coins could indicate under which one the key is].
Ok, I have been silly. I have forgotten to apply the number one rule of puzzle solving: start by first solving a simpler case. There is no point in trying to solve a full chessboard, let's start with a 2x2 board (the 1x1 case is not exactly... interesting).
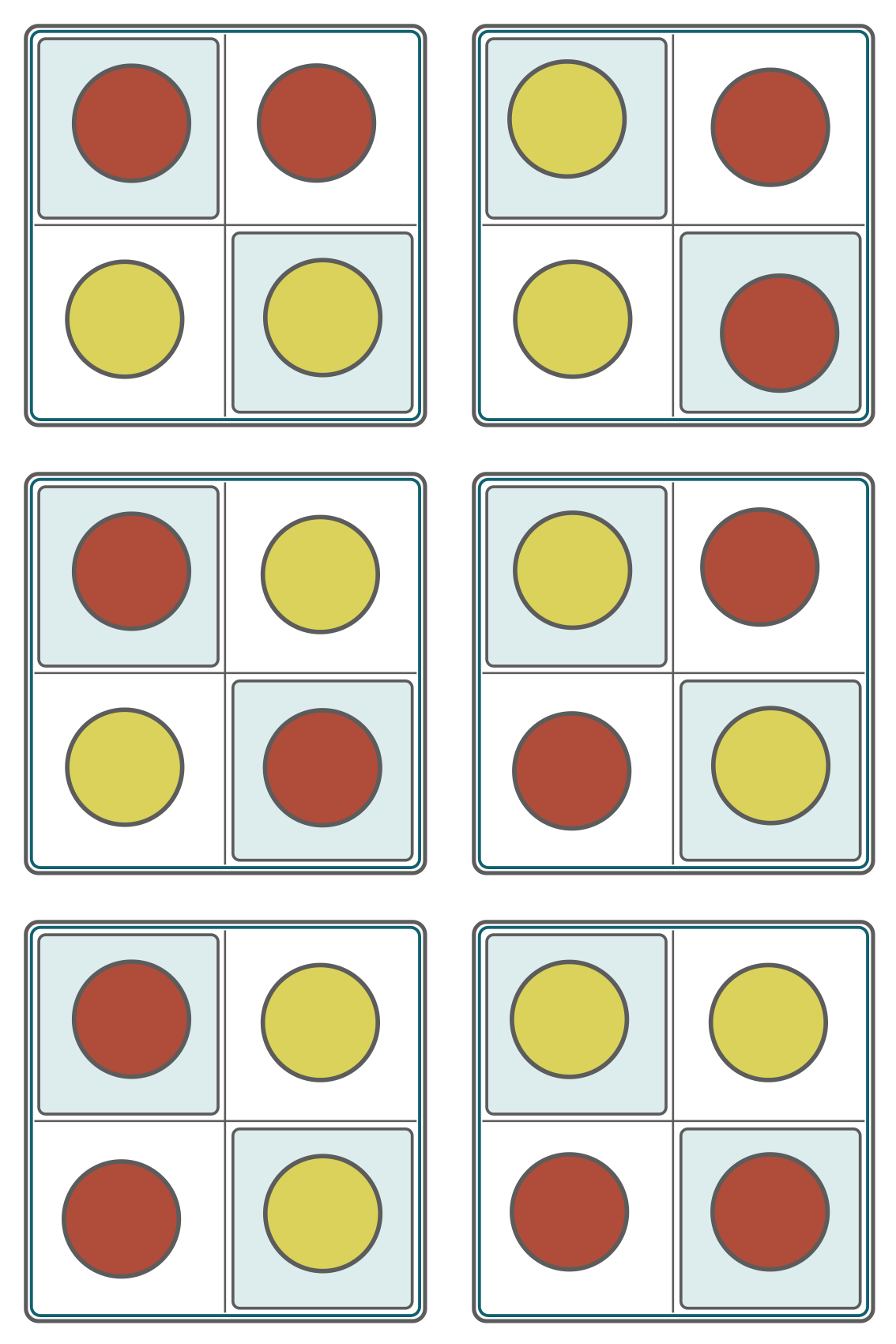
Ah this feels so much simpler already! So in the case where the second player receives a board with one coin flipped up, that indicates where the key is. And we can do the same by symmetry, when there is only one coin flipped down. All we have left to solve is the case when there are two coins flipped up. This corresponds to the situation when there was only one coin flipped up (or down, by symmetry) when the first player was shown the board. The first player gets to chose which other coin will be flipped up. Now, I think I just stumbled upon the key to solve this problem here: The adversary only gets to chose among 4 board states, to create, but the first player, by flipping a coin, creates a board amongst 6 states! There are more ways to flip two coins than there are ways to flip one coin.
So now, we can figure out a strategy. With just the first 4 cases in the figure above, we can decide where is the key as per the figure below. All possibilities for the key position are covered, and all possibilities for the initial coin flipped position are covered. the first player just has to flip the coin that leads to the desired state of the board.
For example if we take the top right case in the figure.... Oh never mind, I just realised that I got something wrong. If the key is in the top left corner, and the adversary flips the bottom right corner coin, there is no way in my schema above to get to tell the second player where the key is. However, I can make use of the bottom two situations as well.
Now I am realising that I have a problem. There are two starting key positions that do not let the first player give enough information for the second player to find the key (the middle ones in the figure above). If the key is in the bottom right corner, then the adversary can flip the bottom-left corner, and there is no coin that the first player can flip to tell where the key is located. Well... unless...
It is time to revise my very first assumption. I wrote above that we will avoid giving a blank state to the first player. Let's not do this, this is wasting information! We will use the blank state to patch the previous example. When the chessboard is blank, it means that the key is under the bottom-right corner. This way when the adversary flips the bottom left coin, we just flip it back to get a blank state. This still leaves us with a few cases unaccounted for...
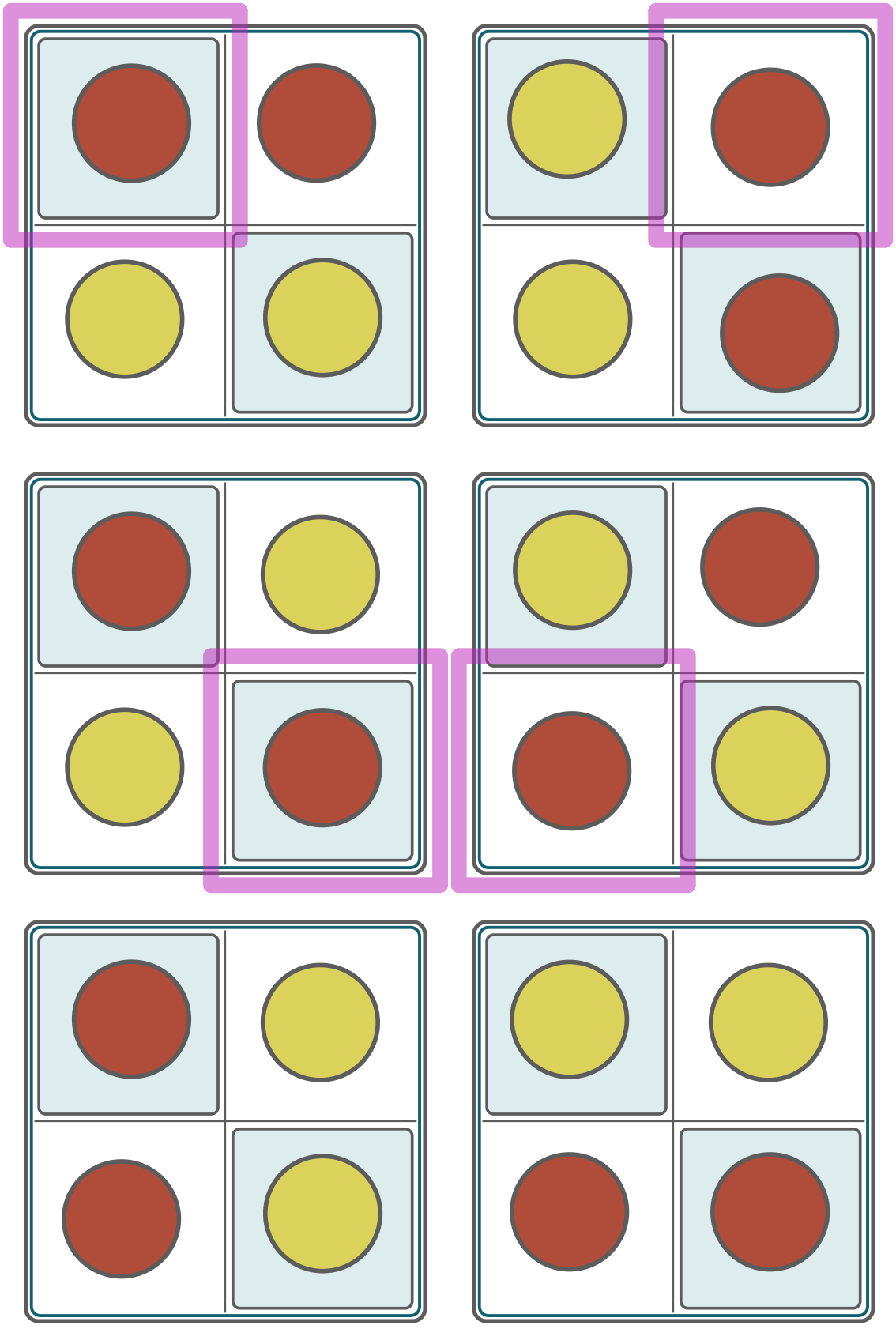
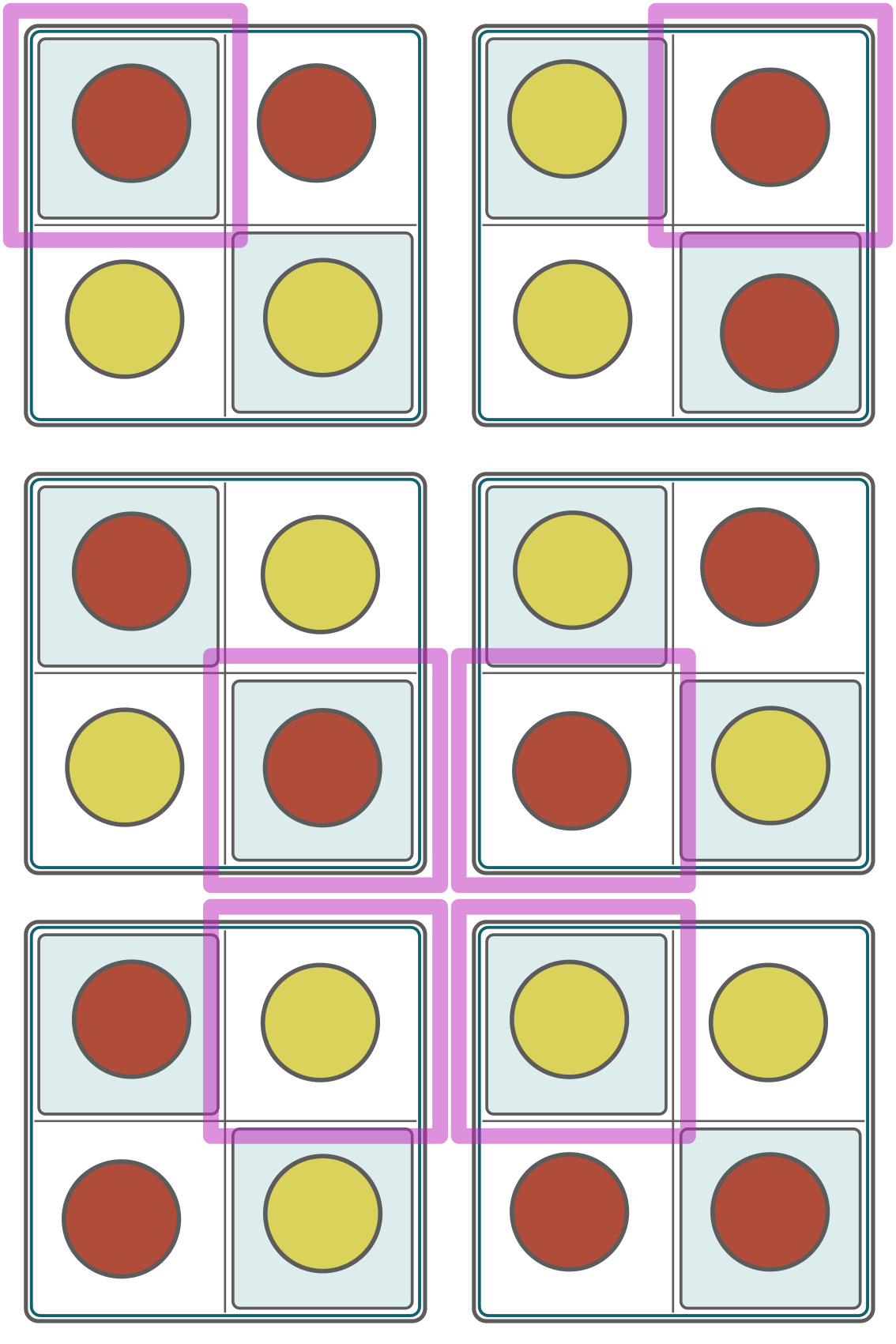
Let's slow down and think about what I have been doing. The case where the key is in the top-left key position is fully covered by my strategy because there are two states of the board for it, and the coins are exactly symmetric. This is important because it means that there is a case that has a black coin on every square, so the first player can always flip another coin to indicate that we are in the (key in the top-left) situation. My examples in the middle do not follow this rule. I think that by fixing them and including the blank states in the strategy, I will have solved the 2x2 case. Let's show the complete strategy.
Now is a good time to take a step back, and see if I can generalise a solution from there on. Let's try to really understand why this works. For each starting position of the key, no matter what the adversary decides, there is a coin that can be flipped to indicate what the key's starting position was. I now I suddenly realise that I have been silly, once again. I have started with the 2x2 case, but this was not the simplest, non-degenerate case! The fact that this is a squared board does not matter for this problem, it could just as well be a 2x1 board! This would have made all the above much simpler to picture and reason about.
So let's do it, let's reason about the 2x1. There are two starting states, the key is either on the right or on the left. Then, the adversary can create 4 different visible board positions. Combined with the key position, that leads to 8 possibilities. When the first player flips a coin, according to the predetermined strategy, the state space is compressed to 4 possibilities, that are all different in terms of the visible features. This is what allows the second player to know where the key is.
Looking at the figure above, we get a necessary condition for the strategy: when there are several positions of the key for the same state of the board, we must flip coins to eliminate all but one position. Now we just need to find a way to do so such that each final state of the board is at most one coin flip away from an original state.
I think it is about time that we move away from chessboards and into the realm of binary numbers. We will encode a state of the board with n squares like so: An integer k represents the position of the key (0 means the first square, 1 means the second square, etc), and an n-digits binary string represents the state of the coins on the board. For example, with a 2x1 board, the possible states of coins are 00, 01, 10, 11. Including the integer representing the board state we have 8 possible states: 0.00, 0.01, 0.10, 0.11, 1.00, 1.01, 1.10, 1.11.
Let's look at the next case, three squares. There are now 24 possible states: 3 key positions times 8 combinations of coins:
0.000, 0.001, 0.010, 0.011, 0.100, 0.101, 0.110, 0.111
1.000, 1.001, 1.010, 1.011, 1.100, 1.101, 1.110, 1.111
2.000, 2.001, 2.010, 2.011, 2.100, 2.101, 2.110, 2.111
I am thinking of many ways to visualise this. The coin positions can be visualised by a 3d cube. Each state can be interpreted as a coordinate in a 3d space. What is nice about this visualisation is that it gives us a graph of the possible transitions. Flipping a coin corresponds to moving from one edge of the cube to an adjacent one.
Note that we can use the same cube visualisation to represent the state of the coins with 3 squares (as above) or the state of the coins + the key with 2 squares (as below). In that case we can mark the solutions. The vertical axis represents the key position. At the bottom, this is when the key is in the first square, at the top this is when the key is in the second square. This gives us a more intuitive understanding of what we are trying to build. We need to find a set of nodes that are exactly one step away from any node we start on, such that there are no two nodes selected that are adjacent vertically (it would mean that two key positions are encoded by the same state of the board).
For the board with 3 squares, we would have to draw a kind of hypercube, which is not handy. Actually, not a hypercube, because the key can be in 3 positions, not 2. But we can represent it with... 3 adjacent cubes! The node selection process can be visualised as in the image below: picking a node means the same nodes in the other cubes become unavailable.
Let's see if we can build our solution using the principles we have derived so far. First we select the board states that directly indicate where the key is: 0.001, 1.010, 2.100, 0.110, 1.101, 2.011
Now we can mark every node that is exactly 1 step away from a solution node.
The only nodes that are not one step away from a solution are the solutions themselves. Now this is a place where I am not certain about the rules, but I assume that the first player must flip a coin, he is not allowed to just leave the board as it was. So we must add solutions that are reachable from these states. Let's give it a try
It turns out that we have a problem. There is only one solution for the first two key positions, and once they are picked there is no solution left for the last key position. It means that if the adversary starts with the key on the third square, one coin down and two coins up, there is nothing the first player can do, assuming that he is not allowed to leave the board as is.
So I think that this questions our initial choice of solutions. Let's go for a more systematic approach. We will try and devise an algorithm that solves this. We start by picking 0.000 as a solution (with no loss of generalisation, by symmetry). This eliminates 1.000 and 2.000. This also makes 0.001, 0.010, 0.100 neighbours of a solution, so I will avoid selecting them for now.
Let's look at the second cube, and here I am tempted to select 1.001 because it will eliminate 0.001 which is already neighbour of a solution, and 1.000 which has been eliminated will become neighbour of a solution.
At this point I am thinking about Gray Code. Gray Code is a way to count binary such that two consecutive strings are always exactly one bit away from each other, surely this will come in handy for this puzzle, especially for dealing with higher dimensions when I can't rely on drawings anymore. But let's continue with the 3d visualisation for now.
Actually, let's stop. I just had a feeling that this won't be possible. For each cube, each node must be the neighbour of a solution. This means that there must be (at least) three solution nodes per cube. There is no way to have 2 solutions, and every node including themselves is the neighbour to another solution. But, each solution eliminates a node in the other cubes. 3 solutions in two cubes eliminate 6 nodes in the third cube, meaning only two nodes left...
So, that means one of these two statements is true:
I got the instruction wrong, and the first player is allowed to not flip a coin
There is something special about the 3x1 case that makes it impossible (the instructions were for a chessboard after all, which implies a square number)
And this is it for my first session. Although this was a single hour of ideation, documenting the process and creating the illustrations from my hand drawing was incredibly time-consuming. To be continued...